Здесь мы сначала докажем теорему Пифагора, а потом применим ее для управления полетом летучей мыши в Scratch. Между делом изучим несколько приемов программирования на Scratch - вдруг кому пригодится? А еще воспользуемся такой полезной штукой, как Декартова система координат.
Займемся теоремой Пифагора
Итак, что такое "теорема Пифагора"?
Теорема Пифагора применяется для прямоугольных треугольников (у которых один из углов равен 90°), и гласит, что сумма квадратов катетов (сторон, прилежащих прямому углу) равна квадрату гипотенузы (стороны, противолежащей прямому углу).
Другими словами, сумма площадей квадратов, построенных на катетах, равна площади квадрата, построенного на гипотенузе. Это можно проиллюстрировать картинкой, которую еще называют "Пифагоровы штаны (на все стороны равны)".
Математически теорема выражается равенством a2 + b2 = c2.
Существует несколько способов доказательства этой теоремы. Я предлагаю вашему вниманию очень изящный и очень наглядный начертательный способ. Считать ничего не придется, зато придется рисовать.
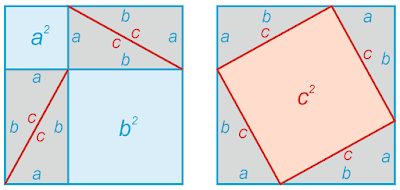
Итак, возьмем треугольник abc (как на картинке) и впишем его двумя способами в квадрат со стороной равной a + b.
Посмотрите внимательно на этот рисунок. Как видите, квадраты ab равны, поскольку их стороны в обоих случая равны a + b. Их площади, соответственно, тоже одинаковы и равны
Далее. В обоих случаях мы вычитаем из площадей квадратов по четыре треугольника abc. Значит, оставшиеся площади равны друг другу. В первом случае остается сумма площадей квадратов а2 и b2, во втором случае - площадь c2. Значит, a2 + b2 = c2. Теорема доказана.
Если вас чем-то не устраивает это доказательство, вы можете поискать более другие в Википедии и во всех остальных интернетах. :)
"Какая связь с летучей мышью, уважаемый?" - спросите вы. А очень простая. Летучая мышь всегда летит по гипотенузе. :)
Займемся летучей мышью
Вообще, эта заметка выросла из поисков решения, когда нужно было заставить объект (спрайт) в Scratch перемещаться по случайным координатам с постоянной скоростью. Сейчас увидим все тоже очень наглядно, на живых летучих примерах.
Запустим Scratch и возьмем летучую мышь.
Для начала заставим ее махать крыльями (я не буду оскорблять ваш интеллект подробным комментированием примеров, сами разберетесь).
Теперь заставим ее перемещаться в точку со случайными координатами. Понимание Декартовой системы координат в данном случае пригодится, но объяснения выходят за рамки этой заметки (и см. выше комментарий про оскорбление интеллекта).
 |
| Кликните для увеличения |
Запускаем. Как мы видим, время перемещения из одной точки в другую у нас одинаковое, а скорость перемещения разная, и зависит от расстояния между случайно выбираемыми точками.
Давайте сделаем так, чтобы скорость полета мыши была всегда одинаковой.
Что такое скорость? Это расстояние, деленное на время. Значит, если нам нужно чтобы скорость была постоянной, нам потребуется каждый раз подставлять в пример выше новое значение времени, зависящее от расстояния, которое мы вычислим по формуле
t = l/v
где t - время, l - расстояние, а v - скорость.
Как вычислить расстояние? Летучая мышь в нашем примере всегда летит по гипотенузе прямоугольного треугольника, что понятно из рисунка.
Как видите, всегда можно достроить прямоугольный треугольник для любых двух точек.
Теперь вычислим расстояние, которое предстоит пролететь, махая крыльями, нашей летучей мыши. Расстояние - гипотенуза прямоугольного треугольника, значит можем посчитать по формуле
l = sqrt((x1 - x2)2 + (y1 - y2)2)
sqrt - обозначение квадратного корня, остальное и так понятно. В некоторых случаях, когда
Вернемся к Scratch. Создадим три переменных: x и y для новых координат, куда устремится наша летучая мышь, и переменную time для времени, которое она потратит на перемещение.
Затем полученное значение l подставим в формулу для времени, и получим такую конструкцию на Scratch. Скорость перемещения возьмем равной 50 "шагам" в секунду.
 |
| Кликните для увеличения |
Можно было бы обойтись без переменной time, но тогда пострадала бы наглядность (как мне кажется), и вся конструкция стала бы еще более громоздкой (к сожалению, в Scratch нет отдельной функции возведения в степень, поэтому приходится обходиться умножением).
Запускаем. Теперь наша летучая мышь летит с постоянной скоростью 50 шагов в секунду в любую случайную точку экрана.
Если у вас возникли вопросы - для начала перечитайте этот материал еще раз. :) Если вопросы не пропали - проведите расчеты при помощи бумажки, ручки и калькулятора с функцией возведения в квадрат и извлечения корня. Если вопросы все еще остались - задавайте их в комментариях.
Сложно? Вовсе нет. Нам с сыном-третьеклассником пришлось потратить около часа на объяснение и доказательство теоремы Пифагора, и примерно столько же - чтобы сделать учебный пример на Scratch.
Зато в результате - практическое применение теоремы Пифагора, совсем не скучное, интерактивное, и не похожее на задачи в учебнике по геометрии. А за одним - и программированием позанимались!





Комментариев нет:
Отправить комментарий